はじめに
こんにちは、駒嶺です。今回はRustでAtCoder Beginner Contest 378に参加しました。
今回からrustfmt(フォーマッター)とClippy(リンター)を導入しました。どちらもRustから提供されているツールです。
詳細は付録D – 便利な開発ツール
A – Pairing

4個のボールから同じ色のペアを捨てる。という操作は何回できるでしょうか?
use proconio::input;
fn main() {
input! {
a: [usize; 4]
}
let mut count = [0; 4];
for ai in a {
count[ai - 1] += 1;
}
let mut ans = 0;
for c in count {
ans += c / 2
}
println!("{}", ans);
}
最初に各色が何個あるかを数えてから、それぞれ2で割って(小数点以下切り捨て)ペアの数を数えました。
各色が何個あるかを数える部分はPythonならCounter()で一発ですが、Rustには同様のものはなさそうです。
B – Garbage Collection

N種類のゴミの回収する頻度qと回収日rが与えられます。
例えば頻度q=7で回収日r=3なら7日ごとの3日目に回収されます。
ゴミtをd日に出した時、回収されるのはいつでしょうか?というクエリにQ回答えます。
解答
use proconio::{input, marker::Usize1};
fn main() {
input! {
n: usize,
qr: [(i64, i64); n],
q: usize,
td: [(Usize1, i64); q]
}
for (t, d) in td {
let (q, r) = qr[t];
if d % q <= r {
println!("{}", d - d % q + r);
} else {
println!("{}", d - d % q + q + r);
}
}
}
12行目 最初にd % qでゴミを出した日dがその周期の何日目なのかを計算し周期中の回収日rより前か後かを判定します。
13行目 回収日より前ならその周期の最初の日(d – d % q)+ 回収日(r)が次の回収日
15行目 回収日より後なら次の周期の最初の日(d – d % q + q)+ 回収日(r)が次の回収日となります。
コンテスト中は上記のコードを提出しましたが、実はこれはifなしでも書くことができます。
解答(ifなし版)
use proconio::{input, marker::Usize1};
fn main() {
input! {
n: usize,
qr: [(i64, i64); n],
q: usize,
td: [(Usize1, i64); q]
}
for (t, d) in td {
let (q, r) = qr[t];
println!("{}", d + (r - d % q + q) % q);
}
}
回収日rを基準に日付を考えるイメージです。
rとdの差分をqの割った正の余りを計算すれば次の回収日まであと何日かが計算できます。
負の数に対する余りを負の値とするか正の値とするかは言語によって異なるところですが、RustではC++と同じく負の値になります。つまり -5 % 4 = -1 です。
Rustで余りを正の値で取りたいときは ((-5 % 4) + 4) % 4 = 3 のようにすればOKです。
ちなみにPythonでは正の値になるようになっていて -5 % 4 = 3 となります。
C – Repeating

正数列AをA1から順に見ていって、その数が初めて登場した場合は-1、すでに登場している場合は直前に登場した位置を答えます。
解答
use proconio::input;
use std::collections::HashMap;
fn main() {
input! {
n: usize,
a: [i64; n]
}
let mut map: HashMap<i64, usize> = HashMap::new();
for (i, ai) in a.iter().enumerate() {
if let Some(last) = map.get(ai) {
print!("{} ", last);
} else {
print!("{} ", -1);
}
map.insert(*ai, i + 1);
}
}
値と直前に登場した位置のHashMapを作りました。
Rustでは無効かもしれないものを扱うためにOption型という便利な列挙型があり、戻り値がOption<T>の関数は値が有効な場合はSome(T)、無効な場合はNoneを返すように実装されます。
11行目 if let Some(last) = map.get(ai) はmap.get(ai)で値が取れたら変数 last にその値を束縛し、以降の処理を行います。
D – Count Simple Paths

H行W列のマス目があり、空きマスと障害物があるマスがあります。
ある空きマスから障害物のあるマスを通らず同じマスを2回以上通らずにピッタリK歩あるくことができるルートの個数を数えます。
解答
use itertools::iproduct;
use proconio::{input, marker::Chars};
fn main() {
input! {
h: usize,
w: usize,
k: usize,
board: [Chars; h]
}
let mut ans = 0;
for (col, row) in iproduct!(0..h, 0..w).filter(|(col, row)| board[*col][*row] == '.') {
ans += search(&board, &[(col as i64, row as i64)], k);
}
println!("{}", ans);
}
fn search(board: &Vec<Vec<char>>, path: &[(i64, i64)], k: usize) -> i64 {
if k == 0 {
return 1;
}
let current = path[path.len() - 1];
let mut a = 0;
for to in [(1, 0), (-1, 0), (0, 1), (0, -1)] {
let (col, row) = (current.0 + to.0, current.1 + to.1);
if col >= 0
&& col < board.len() as i64
&& row >= 0
&& row < board[0].len() as i64
&& !path.contains(&(col, row))
&& board[col as usize][row as usize] == '.'
{
a += search(board, &[path, &[(col, row)]].concat(), k - 1);
}
}
a
}
これはまさしくBPF(深さ優先探索)ですね。
18行目 search()という名前の再帰関数でBPFを実装しています。
引数はマス目とこれまで通った道と残り歩数です。
現在地から各方向のマスに対してそのマスが歩けるかどうか(範囲内でまだ歩いていないマスで障害物物がないマス)を判定し、歩けるならそのマスをpathに追加し、歩数を消費して再度search()を呼び出します。
12行目 iproduct!は複数の添え字での多重ループをまとめて書けるマクロです。
use itertools::iproduct;
fn main() {
for (col, row) in iproduct!(0..5, 0..10) {
print!("これと");
}
for col in 0..5 {
for row in 0..10 {
print!("これは同じ");
}
}
}
アルゴリズム自体はすぐに思いついたのですが、Rustでの実装に手間取りコンテスト中に解答できませんでした。
コンテスト結果
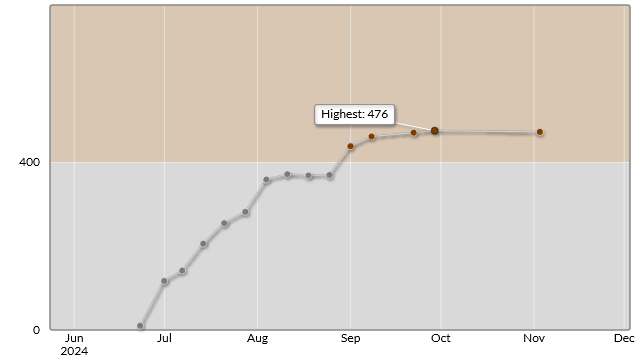
今回のA~D問題は簡単だったのでDが解けなかったのが痛いです。
アルゴリズムは分かってもRustでの実装につまづいている時間が長くもどかしい思いをしています。
Rustに慣れるまで精進します。
おわりに
本ブログを通じて私と一緒に競技プログラミングの世界を楽しんでいただければ幸いです。
また、各種ご支援させていただきますので、お気軽に「お問い合わせフォーム」よりお問い合わせください。