【AtCoder 緑色を目指して】ABC369【競技プログラミング】

技術ブログ 競技プログラミング

はじめに

こんにちは、駒嶺です。今回はAtCoder Beginner Contest 369の所感です。
今回もPythonで解いていきます。

A – 369

整数A、Bが与えられたとき、それらと等差数列を作れる整数xは何通りあるでしょうか？

A, B = map(int, input().split())

print(1 if A == B else 2 if (A - B) % 2 else 3)

A=Bの時はx=A=Bで等差0の数列しか作れないので1通り
A≒BでAとBの差が2の倍数でない時はAとBの左側と右側にxを置けるので2通り
A≒BでAとBの差が2の倍数の場合は上記に追加でAとBの真ん中にxを置けるので3通り
となります。

B – Piano 3

高橋君は横一列に並んだ100個の鍵盤からなるピアノの鍵盤を1つずつ押して演奏を行います。
i回目に押す鍵盤の番号とそれを押す手が指定されています。
手を動かすと鍵盤の番号の差だけ疲労度が溜まります。
最初の手の位置を自由に決めていいとき、演奏後の最小の疲労度を求めてください。

解答

N = int(input())

hands = {}
cnt = 0
for _ in range(N):
    A, S = input().split()
    A = int(A)
    hand = hands.get(S,A)
    cnt += abs(hand - A)
    hands[S] = A

print(cnt)

問題の読解が難しかったです。疲労度の最小値と書いてありますが選べるのは最初の手の位置だけで、鍵盤を押す順番や押す手は変更不可です。
最初の手の位置はその手は最初に押す鍵盤の上とするのが一番疲れずに済みますね。
ということで左右の手の位置を辞書に格納し、その手が最初に使われた時（値が空の時）はその位置を初期位置とするようにして疲労度をシミュレートしました。

C – Count Arithmetic Subarrays

長さ N の正整数列 Aが与えられます。その中で等差数列となっている範囲を何通りあるでしょうか？
特に長さ1の数列は常に等差数列です。

解答

N = int(input())
A = list(map(int, input().split()))

cnt = 1
l = 0
r = 0
diff = 0
while l < len(A) - 1:
    diff = A[l + 1] - A[l]
    r = l + 1
    while True:
        if r > len(A) - 2:
            break

        if A[r + 1] - A[r] == diff:
            r += 1
        else:
            break
    cnt += (r-l+1)*(r-l+2)//2 - 1
    l = r

print(cnt)

しゃくとり法ですね。
この問題で言えば範囲の左端と右端を変数L,RとしてRを1つずつ動かしながら等差数列になっている範囲を探ります。
そして等差数列が終了したらL=Rとします。
このLとRの動き方がしゃくとり虫っぽいのでしゃくとり法です。

私の解答のコードではRを1つずつ動かしながらA[R+1]を含めても等差数列になっているかどうかを判定しています。A[R+1]とA[R]の差が公差と一致しなければA[L]～A[R]の間までが等差数列になっていると決定します。
そして一つの等差数列の中には等差数列が複数含まれているのでその個数をLとRの値から求めています。
例えばA = [1, 3, 5, 5, 7, 8]の時、L=0、R=0から始めると
R=0の時 [1, 3]は等差数列
R=1の時[1, 3, 5]は等差数列
R=2の時[1, 3, 5, 5]は等差数列ではありません。
よって[1, 3, 5]までの範囲が等差数列とわかりましたが、この等差数列の中には
[1], [1, 3], [1, 3, 5]
[3], [3, 5]
[5]
の合計6つの等差数列があります。
合計いくつの等差数列があるのかは1から「等差数列の長さ」までの総和で求められます。

D – Bonus EXP

高橋君はN匹のモンスターに順番に出会います。
それぞれのモンスターについて逃がすか倒すか選ぶことができ、倒すとモンスター毎の経験値が貰えます。
ただし、モンスターを倒すのが偶数回目の場合、得られるそのモンスターから経験値が倍になります。
高橋君が得られる経験値の最大値を求めます。

解答

N = int(input())
A = list(map(int, input().split()))

dp = [[0,0] for _ in range(N+1)]
dp[0][1] = -float('INF')
for i, a in enumerate(A):
    dp[i+1][0] = max(dp[i][0], (dp[i][1] + a * 2))
    dp[i+1][1] = max((dp[i][0] + a), dp[i][1])

print(max(dp[-1]))

動的計画法*1一閃！
各回ごとにその回終了時に現在の倒したモンスター数が偶数回の場合の最大経験値と奇数回の場合の最大経験値をそれぞれ保持する二次元配列を用意します。
そうしたら後はモンスターに順に出会いながら倒した回数が偶数になる場合、倒した回数が奇数になる場合それぞれで最大値を更新していけば高橋君が得られる経験値の最大値が求められます。

コンテスト結果

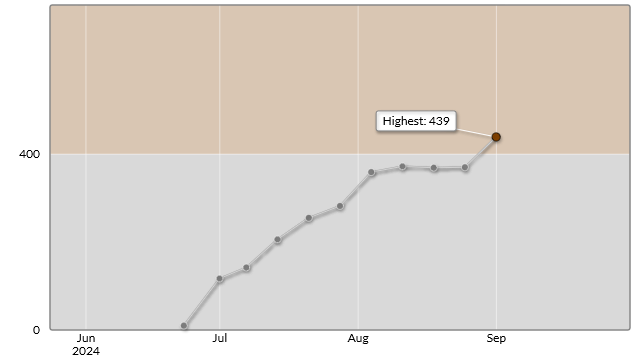
今回はA～Dまでの4完でそこそこ満足のいく結果になりました。レーティングも茶色に乗りました。
C問題、D問題をスパッと解けて楽しかったです。勉強したアルゴリズムが役に立ちました。
D問題を解いた後、グラフ系問題のE問題を飛ばして動的計画法で解けそうなF問題にも挑戦したのですが、そちらは実装しきれず時間切れとなったので少し悔しさを残しています。

おわりに

次回はABC370の記事を投稿します。
本ブログを通じて私と一緒に競技プログラミングの世界を楽しんでいただければ幸いです。
また、各種ご支援させていただきますので、お気軽に「お問い合わせフォーム」よりお問い合わせください。

お問い合わせ
　業務実績　
  1. DP(Dynamic Programming)とも呼ばれる。表を埋めていく形で計算をすすめ、冗長な計算をはぶくアルゴリズム。 ↩︎

関連記事