はじめに
こんにちは、駒嶺です。今回はAtCoder Beginner Contest 366の所感です。
今回もPythonで解いていきます。
A – Election 2

AtCoder 市では市長選挙が行われています。候補者は高橋氏と青木氏です。
開票の途中経過が与えられるので現時点で勝敗が確定しているか判定します。
解答
N, T, A = map(int, input().split())
print("Yes" if T*2 > N or A*2 > N else "No")現時点でどちらかが過半数の票を得ている場合はその候補者が勝利で確定するのでYes。そうでないならNoです。
Nは奇数なので同数にはなりません。
B – Vertical Writing

横書きの文章を縦書きに直します。空白は*で埋める必要があります。
イメージしにくいので入力例と出力例を見てみましょう。
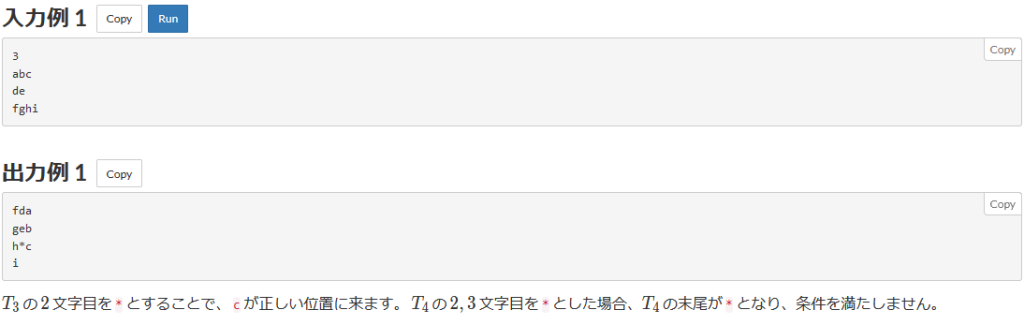
横書きが縦書きになっていますね。
解答
N = int(input())
T = [input() for _ in range(N)]
length = [len(s) for s in T]
for i in range(max(length)):
for j in range(N-1, -1 ,-1):
if i < len(T[j]):
print(T[j][i], end="")
elif i < max(length[:j] or [0]) :
print("*", end="")
print("")*で空白を埋めるところでもたついてしまいました。縦書きにしたときに自分より右に文字がある場合は*を入れるようにしています。
解説では先に*で文字数を合わせて、最後に不要な*を取り除く方法が解説されていました。
C – Balls and Bag Query

袋の中に整数が書かれたボールを入れる。出す。袋の中のボールの種類を答える。この3つのどれかを行うクエリを最大で2×10^5回実行します。
解答
Q = int(input())
d = {}
for _ in range(Q):
a, *b = map(int,input().split())
if a == 1:
d[b[0]] = d.setdefault(b[0],0) + 1
elif a == 2:
if d[b[0]] >= 2:
d[b[0]] -= 1
else:
d.pop(b[0])
elif a == 3:
print(len(d))ボールの個数を辞書で管理しました。
ボールが0個になるときは辞書からpop()しておけばボールの種類は辞書のlen()で求められます。
D – Cuboid Sum Query

3次元の表が与えられます。表には整数が書かれています。
表の範囲が与えられるのでその中に書かれている数をすべて足してください。というクエリを最大2×10^5回実行します。
解答(TLE)
N = int(input())
A = [[list(map(int, input().split())) for _ in range(N)] for _ in range(N)]
Q = int(input())
for i in range(Q):
Lx, Rx, Ly, Ry, Lz, Rz = map(int, input().split())
output = 0
for i in range(Lx-1, Rx):
for j in range(Ly-1, Ry):
for k in range(Lz-1, Rz):
output += A[i][j][k]
print(output)いったん言われたとおりに書いてみました。
与えられた範囲の数をすべて足して回答する。を毎回行っています。
実行時間は3315msでTLE1となってしまいました。
解答(コンテスト終了後)
N = int(input())
A = [[list(map(int, input().split())) for _ in range(N)] for _ in range(N)]
Q = int(input())
ac = [[[0] * (N + 1) for _ in range(N + 1)] for _ in range(N + 1)]
for i in range(1,N + 1):
for j in range(1,N + 1):
for k in range(1,N + 1):
ac[i][j][k] = ac[i][j][k-1] + A[i-1][j-1][k-1]
for i in range(1,N + 1):
for j in range(1,N + 1):
for k in range(1,N + 1):
ac[i][j][k] = ac[i][j-1][k] + ac[i][j][k]
for i in range(1,N + 1):
for j in range(1,N + 1):
for k in range(1,N + 1):
ac[i][j][k] = ac[i-1][j][k] + ac[i][j][k]
for i in range(Q):
Lx, Rx, Ly, Ry, Lz, Rz = map(int, input().split())
Lx, Ly, Lz = Lx - 1, Ly - 1, Lz - 1
print(
ac[Rx][Ry][Rz]
- ac[Lx][Ry][Rz]
- ac[Rx][Ly][Rz]
- ac[Rx][Ry][Lz]
+ ac[Lx][Ly][Rz]
+ ac[Lx][Ry][Lz]
+ ac[Rx][Ly][Lz]
- ac[Lx][Ly][Lz]
)最近読んだ「競技プログラミングの鉄則」という本に1次元の累積和と2次元の累積和の解説がありました。
この問題はそれをさらに拡張して3次元の累積和を使えば解けますね。
3次元の累積和を作るところまではできていたのですが、26行目以降の累積和から答えを出すところをこねくり回している内にコンテストが終了してしまいました。
累積和とは
数値の配列Aに対して累積和の配列Sを作ります。
A = [A0, A1, A2, A3, A4, A5]
S = [S0, S1, S2, S3, S4, S5]
配列Sの要素Siは配列AのA0からAiまでの総和です。
この配列Sを使うと、例えばA2からA4までの範囲の総和(A2 + A3 + A4)をS4 – S1で一発で求めることができます。
S4 – S1 = (A0 + A1 + A2 + A3 + A4) – (A0 + A1) = A2 + A3 + A4
配列Aの要素数をNとすると配列SはO(N)で作成できます。累積和を作ってしまえば配列のある範囲総和はN(1)で求められるため、配列のある範囲の合計を何度も求めたいときには累積和が有効です。
コンテスト結果

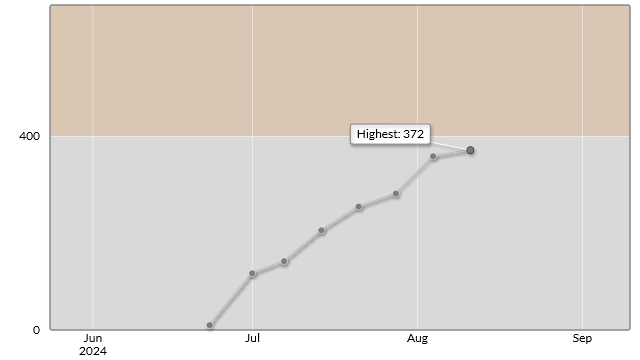
D問題が間に合わず3完でした。B問題でもたついていたのが悔やまれます。
D問題も解き方自体は思いついたので勉強の成果は出ていると思います。
あとはコンテスト中にコードを書ききる力をつけるため精進2あるのみでしょうか。
おわりに
次回はABC367の記事を投稿します。
本ブログを通じて私と一緒に競技プログラミングの世界を楽しんでいただければ幸いです。
また、各種ご支援させていただきますので、お気軽に「お問い合わせフォーム」よりお問い合わせください。
