【AtCoder 緑色を目指して】ABC365【競技プログラミング】

技術ブログ 競技プログラミング

はじめに

こんにちは、駒嶺です。今回はAtCoder Beginner Contest 365の所感です。
今回もPythonで解いていきます。

A – Leap Year

うるう年を考慮して1583年～2023年のある年の日数を求めなさい。
そういえば今年2024年はうるう年ですね。

解答

Y = int(input())

if Y % 400 == 0:
    print(366)
elif Y % 100 == 0:
    print(365)
elif Y % 4 == 0:
    print(366)
else:
    print(365)

問題分の通りにif文を書きました。

B – Second Best

整数列で2番目に大きい要素は何番目の要素でしょうか？
値の重複はありません。

解答

N = int(input())
A = list(map(int, input().split()))

second = sorted(A)[-2]
for i in range(len(A)):
    if A[i] == second:
        print(i+1)
        break

配列をソートして2番目に大きい値を特定。
そしてforでその値が配列の何番目か探しています。
何番目か探すところはindex()を使用するほうが簡単でしたね。

C – Transportation Expenses

N人にそれぞれX円まで交通費の補助を出します。
予算を超えないように交通費補助額の上限値を決めてください。
上限値をいくら増やしても予算を超えない場合はそのことを報告します。

解答

import bisect
N, M = map(int, input().split())
A = list(map(int, input().split()))

if sum(A) <= M:
    print("infinite")
    exit()

A.sort()
len_A = len(A)
lo = -1
hi = 10**10
while lo + 1 < hi:
    x = (lo + hi) // 2
    border = bisect.bisect_left(A, x)
    if sum(A[:border]) + (len_A - border) * x > M:
        hi = x
    else:
        lo = x
print(lo)

「上限値をいくら増やしても予算を超えない場合」とは交通費の合計が予算以内の場合です。
交通費全額補助ですね。最初に判定して早期リターン（早期exit？）してます。

さて、全額補助できない場合、支払い総額が予算を超えないギリギリの補助額上限値は二分探索で求められます。
補助額の上限値を大きくするほど支払う総額が大きくなります。つまり広義単調増加ですね。
広義単調増加なら二分探索が使えます。
二分探索とは何かについては前回のABC364 D問題で触れています。

私の解答では仮決めした補助額の上限値xから支払い総額を求めるところで複雑な実装をしてしまいました。
border = bisect.bisect_left(A, x)で補助額上限を超える範囲を特定し
sum(A[:border]) + (len_A – border)で補助額の支払い総額を求めていますが
単にsum(min(x,a) for a in A)とするだけでよかったです。
前回のABC364 D問題が二分探索を二重に行う問題だったのでそれに引っ張られました。

D – AtCoder Janken 3

高橋君と青木君がN回じゃんけんをしました。
高橋君の出した手は次の条件を満たします。
・高橋君は1回も負けなかった。
・高橋君は連続で同じ手を出さなかった。
青木君が出した手が与えられるので、高橋君が勝った回数としてありえる最大値を求めます。

高橋君は連続で同じ手を出さないという縛りの中、最大で2×10^5回連続でじゃんけんに負けなかったことになりますね。じゃんけんマスター高橋君。

解答

N = int(input())
S = input()
dp = [[0,0,0] for _ in range(N+1)]
for i in range(len(S)):
    aoki = S[i]
    if aoki == "R":
        dp[i+1][0] = max(dp[i][1], dp[i][2])
        dp[i+1][1] = max(dp[i][0], dp[i][2]) + 1
        dp[i+1][2] = -1
    elif aoki == "P":
        dp[i+1][0] = -1
        dp[i+1][1] = max(dp[i][0], dp[i][2])
        dp[i+1][2] = max(dp[i][0], dp[i][1]) + 1
    elif aoki == "S":
        dp[i+1][0] = max(dp[i][1], dp[i][2]) + 1
        dp[i+1][1] = -1
        dp[i+1][2] = max(dp[i][0], dp[i][1]) 

print(max(dp[-1]))

動的計画法（DP）で解けます。※動的計画法となにかについては後述
「i回目のじゃんけんで高橋君がR、P、Sを出した場合にあり得る最大勝利数」を要素にもつ二次元配列を作ります。
そうして最後に「i回目のじゃんけんで高橋君がR、P、Sを出した場合にあり得る最大勝利数」のうち最大のものを出力します。
「i+1回目のじゃんけんで高橋君がR、P、Sを出した場合にあり得る最大勝利数」はi回目の結果を参照して求められます。
青木君がRを出した時の場合のコードを見てみます。

if aoki == "R":
        dp[i+1][0] = max(dp[i][1], dp[i][2])
        dp[i+1][1] = max(dp[i][0], dp[i][2]) + 1
        dp[i+1][2] = -1

i+1回目のじゃんけんで高橋君がRを出したときにあり得る最大勝利数 dp[i+1][0] は、
i回目で高橋君がPを出していた時にありえる最大勝利数 dp[i][1]
i回目で高橋君がSを出していた時にありえる最大勝利数 dp[i][2]
の大きい方の値です。つまり直前の勝利数の内、大きいほうをそのまま引き継ぎます。
高橋君は連続で同じ手を出せないのでi回目で高橋君がRを出していた時については考えません。

i+1回目のじゃんけんで高橋君がPを出したときにあり得る最大勝利数 dp[i+1][1] は、
i回目で高橋君がPを出していた時にありえる最大勝利数 dp[i][1]
i回目で高橋君がSを出していた時にありえる最大勝利数 dp[i][2]
の大きい方の値+1 です。今回RにPを出して勝利数が1増えたので+1しています。

i+1回目のじゃんけんで高橋君がPを出したときにあり得る最大勝利数 dp[i+1][2] は…
あり得ませんね。高橋君はじゃんけんに負けません。
この場合はdp[i+1][2]に-1を設定します。そうすればi+2回目のじゃんけんの際にmax関数を使用したときに弾かれてくれます。最大値を求めているときは値としてあり得ない小さい値を設定すればOKです。

同じことを青木君がP、Sを出した場合についても実装しています。
じゃんけん完了後のdp配列の中身を出力してみるとこんな感じです。

青木君の手：PRSSRS
高橋君の手
 R   P   S
[0,  0,  0]
[-1, 0,  1]
[1,  2, -1]
[3, -1,  2]
[3, -1,  3]
[3,  4, -1]
[5, -1,  4]

動的計画法とは

細かくアルゴリズムが定義されているわけではなく、下記2条件を満たすアルゴリズムの総称である。

  1. 帰納的な関係の利用：より小さな問題例の解や計算結果を帰納的な関係を利用してより大きな問題例を解くのに使用する。
  2. 計算結果の記録：小さな問題例、計算結果から記録し、同じ計算を何度も行うことを避ける。帰納的な関係での参照を効率よく行うために、計算結果は整数、文字やその組みなどを見出しにして管理される。
ja.wikipedia.org/wiki/動的計画法

Dynamic Programmingの略でDPとも呼ばれます。
簡単な例として動的計画法でフィボナッチ数列のN番目の項を求めるコードを見てみましょう。

N = 10
fn = []
fn.append(0)
fn.append(1)
for i in range(2,N):
    fn.append(fn[i-2] + fn[i-1])

print(fn) #[0, 1, 1, 2, 3, 5, 8, 13, 21, 34]

そこまでの各項の値を格納した配列 fn を使用し、i番目の項をfn[i-2] + fn[i-1]で求めています。
このようにそこまでの計算結果を記録しておいて再利用するといった手法のことを動的計画法と呼びます。結構定義が広いです。

コンテスト結果

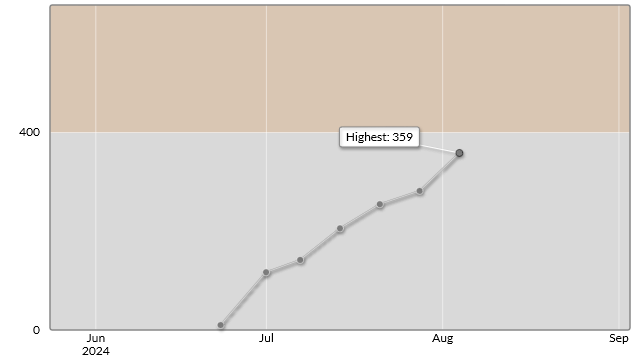
D問題を解いたところでタイムアップとなり4完でした。緑色を目指すにあたってD問題まで解くことを目標にしているので満足です。
パフォーマンスは緑色（800）にギリギリ届かず797でした。
C問題では直近ABC364のD問題で出た二分探索が出てきたことには驚きました。ただ今回は前回よりもどこを二分探索するのかわかりやすい問題でしたね。復習しておいてよかったです。
D問題の動的計画法についてもABCでは度々出ています。私は解いていませんがABC364のE問題も動的計画法でした。応用範囲が広いテクニックなので頻出です。D問題のDはDP（動的計画法）のDと言われるほどです。
この辺りのテクニックを身につければ緑色に到達できるのではないかと思っています。

おわりに

次回はABC366の記事を投稿します。
本ブログを通じて私と一緒に競技プログラミングの世界を楽しんでいただければ幸いです。
また、各種ご支援させていただきますので、お気軽に「お問い合わせフォーム」よりお問い合わせください。

お問い合わせ

　業務実績　

関連記事