はじめに
こんにちは、駒嶺です。今回はAtCoder Beginner Contest 363の所感です。

A問題らしい簡単な問題でした。ちなみに高橋君とはAtCoder株式会社の代表取締役、高橋直大さんのことです。太郎君のような扱いをされており問題文によく出てきます。
解答
R = int(input()) print(100 - R % 100)
余りを使ってきれいに書くことができました。if文で分岐してもOKでしょう。

1日に1ずつ(単位不明)髪が伸びる呪いの日本人形がN人あって、それぞれ髪の長さが与えられます。
髪の長さがTを超えた人形がP人を超えるのは何日後でしょうか
解答
N, T, P = map(int, input().split()) L = list(map(int, input().split())) L.sort() print(max(T - L[-P],0))
NとTの数が100以下なので実際にN人の人形の髪を1ずつ伸ばすシミュレーションをしてもいいですが、髪がP番目に長い人形の髪が何日目に長さTに到達するかを考えるほうが計算量もコードの長さも少なく済みました。
初日の時点で条件を満たしている場合0を出力せよ。とあるのでmax関数で0と比較しています。(初日の時点で長さTを超えているなら、長さTになる日は初日より前、つまり負の値になります。)

今回多くのPython使いを苦しめた問題です。ABC363にちなんで回文がテーマのようです。
回文の判定自体は過去問で実装したことがありました。こんな感じの実装になります。
S = input()
for i in range(len(S)//2):
if S[i] != S[- i - 1]:
print("No")
break
else:
print("Yes")さて、問題文に戻ります。
長さNの文字列Sを並び替えて得られる文字列のうち、長さKの回文を部分文字列として含まないものの個数を求めろ。
とのことですが、これは真面目にSを並び替えた文字列すべてに対して長さKの部分文字列が回文かどうかの判定をするしかなさそうです。
これが最悪の場合どれだけの計算量になるのか計算してみましょう。
長さNの文字列を並び替えた文字列はN!通り。
長さNの文字列に対して長さKの部分文字列の取り方はN-K+1通り。
そして長さKの文字列に対して回文判定を行う場合Kが奇数なら(K-1)/2回、偶数ならK/2回ループすることになります。
Nが10、Kが6の時を考えると10!通りの文字列に対してそれぞれ5通りの部分文字列を取り、部分文字列それぞれに3回ループを行います。
10! × 5 × 3 = 3628800 × 15 ≒ 5×10^7
Python(PyPy)は実行制限時間の2秒の間に10^8回ほど計算ができると言われています。
1ループ中に何回か処理があることを考えると2秒以内に間に合わないでしょう。
ということで私はこの問題をスキップすることにしました。
コンテスト終了後に解説を見ると、Pythonではやはり厳しいようでPythonで書いたコードを生成AIを使用してC++のコードに変換する方法が紹介されていました。※問題文を直接与えなければ生成AIの使用は認められています。
私がこれまでに解いた問題では遭遇したことがなかったのですが、こういったことがあるので競技プログラミングでは処理速度が速いC++が有利とされています。

また回文です。C問題の考察で回文にはもうずいぶん嫌な印象を持っています。
問題文はシンプルで、小さい方からN番目の回文になっている数字を求めろというものです。
しかしNが最大1018とかなり大きめ
解答(不正解)
N = int(input())
if N <= 10:
print(N-1)
exit()
digit = 2
cnt = N - 10
while True:
a = 10**((digit + 1) // 2) - 10**(((digit + 1) // 2)-1)
if cnt - a <= 0:
break
else:
cnt -= a
digit += 1
ans_list_r = list("1".zfill((digit // 2 + 1)))
cnt -=1
cnt_str = str(cnt)
for i in range(len(cnt_str)):
if i == 0:
ans_list_r[i] = str(int(cnt_str[i])+1)
else:
ans_list_r[i] = str(int(cnt_str[i]))
ans = "".join(ans_list_r[:-(digit % 2)]) + "".join(ans_list_r[::-1])
print(ans)コンテスト時間中に正解までもっていけませんでした。
このコードでやりたかったことを説明します。
まず、与えられたNに対して回答となる回文数が何桁なのかを計算します。
桁数ごとに回文数が何通りあるのかは実際に計算してみると簡単です。
1桁なら0~9の10通り
2桁なら11~99の9通り
3桁なら101からスタートして真ん中の0が0~9の10通り、端が1~9の9通りで掛けて90通り
4桁も同様に90通り
5桁なら10001からスタートして真ん中、その隣、端で10通り×10通り×9通りで900通り
6桁も同様に900通り
これだけやれば法則性が見えてきます。桁数をdとしてその桁の回文数は
dが奇数なら9×10^(d+1)/2-1通り
dが偶数なら9×10^d/2-1通り
となります。※1桁の場合は0が入るので例外
ここまでくればあと一息です。与えられたNに対して、1,9,9,90,90,900,900…と引いていって引けなくなったら回答の回文数の桁数が確定。
その桁数の回文数の最初の数100…001とNから1,9,9,90,90,900,900…と引いていった余りをいい感じにすればN番目の回文数が求められます!
といった考察はできていたのですが、最後のいい感じにしてN番目の回文数を求めるところの実装に手間取って時間切れとなりました。
解答
N = int(input())
if N == 1:
print(0)
exit()
digit = 1
cnt = N - 1
while True:
a = 9 * 10**((digit - 1) // 2)
if cnt - a <= 0:
break
else:
cnt -= a
digit += 1
cnt -= 1
s = str(cnt + 10**((digit - 1) // 2))
print(s + s[::-1][digit % 2:])コンテスト終了後に解説を見ながら書いたコードも載せておきます。
後半のいい感じにして回文数を出す部分がかなりスッキリしています。
コンテスト中の私のコードでは1を0埋めした文字列をリストにして…などとやっていたのですが、シンプルに10^桁数//2を余りに足すだけでよかったです。そうすると10036のような数値が得られるので、それを反転してくっつければ100363001のような回文数が得られます。
おわりに
結局CもDも解けずにAとBの2完でした。Ratingは255に上がり、パフォーマンス(今回の結果のみでの推定Rating)は茶色相当583。目標の緑色(Rating800)には遠いです。
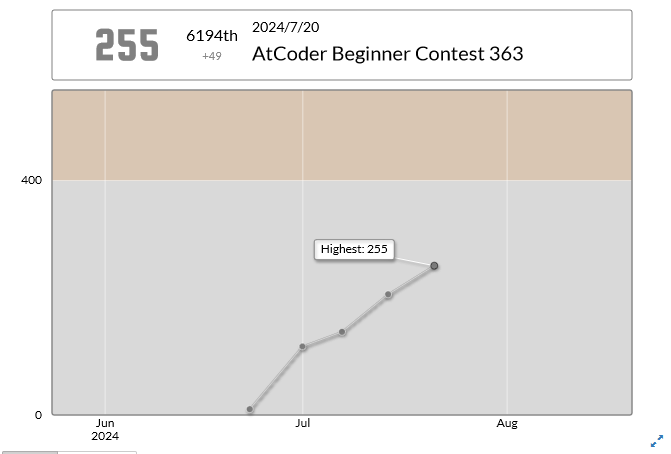

緑色目指して精進します。
次回はABC364の記事を投稿します。
本ブログを通じて私と一緒に競技プログラミングの世界を楽しんでいただければ幸いです。
また、各種ご支援させていただきますので、お気軽に「お問い合わせフォーム」よりお問い合わせください。
