【AtCoder 緑色を目指して】ABC364 Python【競技プログラミング】

技術ブログ 競技プログラミング

はじめに

こんにちは、駒嶺です。今回はAtCoder Beginner Contest 364の所感です。
今回もPythonで解いていきます。

A – Glutton Takahashi

N個の料理を順番に食べようとしますが、甘い料理を2つ連続で食べると高橋君は気持ち悪くなってしまいその後の料理が食べられなくなってしまいます。
高橋君はすべての料理を食べきれるでしょうか？

高橋君は甘いものが連続しなければいくらでも食べられるようですね。すごい

解答

N = int(input())

prev = ""

for _ in range(N-1):
    now = input()
    if  now == "sweet" and prev == "sweet":
        print("No")
        break
    else:
        prev = now
else:
    print("Yes")

forで料理を次々食べながら直前の料理と今の料理が両方甘い場合はNoを出力してループを終了。for文にelseをつけるとループが最後までbreakされなかった場合のみ行う処理を書けます。
問題は高橋君が気持ち悪くなってしまうかどうかではなくすべての料理を食べきれるかどうかなので、最後の料理で高橋君が気持ち悪くなっても関係ありません。よってループはN-1回まで。

B – Grid Walk

2Dのマップと上下左右への移動コマンドが与えられます。
高橋君は初期座標(Si, Sj)から移動コマンドに従って移動します。
ただし、移動先がマップの外の場合または空きマス”.”でない場合は移動できません。
移動コマンドを実行し終えたあと高橋君はどこにいるでしょうか？
移動コマンドはLRUDの文字列で表され、マップはこんな感じです。

....
.#..
...#
....

解答

H, W = map(int, input().split())
Si, Sj = map(int, input().split())
C = ["#"*(W + 2)] + [("#" + input() + "#")  for _ in range(H)] + ["#"*(W + 2)]
X = input()
for i in range(len(X)):
    if X[i] == "L":
        if C[Si][Sj - 1] == ".":
            Sj -= 1
    elif X[i] == "R":
        if C[Si][Sj + 1] == ".":
            Sj += 1
    elif X[i] == "U":
        if C[Si - 1][Sj] == ".":
            Si -= 1
    elif X[i] == "D":
        if C[Si + 1][Sj] == ".":
            Si += 1

print(Si, Sj)

判定を簡単にするためマップを”#”で囲んでみました。マップ端の見えない壁を見える壁に置き換えたとも言えます。
こんな感じです。

######
#....#
#.#..#
#...##
#....#
######

あとは移動コマンドで分岐して実際に高橋君を動かしてみるだけです。
…なんですが、私はこの問題で40分ほど時間を使ってしまいました。
というのも問題文の後には入力例と出力例がいくつか与えられるので、コードの提出前にそれらを使ってローカルでテストをしていた際に入力例と出力例のセットを間違えて「入力と出力が一致しないな～」としばらくデバック作業を続けていました。一致しなくて当然です。
今回のコンテストではここで浪費した時間が順位にかなり響いてしまいました。

C – Minimum Glutton

N個の料理があり、それぞれ甘さとしょっぱさを持っています。
高橋君は甘さの合計がX、しょっぱさの合計がYを超えるまで料理を食べます。
料理を好きな順番で食べていいとき高橋君が食べられる最小の皿数を求めます。

解答

N, X, Y = map(int, input().split())
A = list(map(int, input().split()))
B = list(map(int, input().split()))

ate_A = 0
for i in sorted(A)[::-1]:
    ate_A += 1
    X -= i
    if X < 0:
        break

ate_B = 0
for i in sorted(B)[::-1]:
    ate_B += 1
    Y -= i
    if Y < 0:
        break

print(min(ate_A, ate_B))

甘さとしょっぱさで分けて考えれば簡単です。
料理を甘さが大きい順に並び替えて順に食べていき、甘さの限界Xを超えるまでに何皿食べられるかカウントします。
同じことをしょっぱさでも行い、甘さで限界を限界を超えたときの皿数としょっぱさで限界を超えた解きの皿数のうち、小さい方が答えです。

D – K-th Nearest

数直線上に点がA1～ANのN個あります。
ここで以下のクエリがＱ回与えられます。
　座標Bと整数Kが与えられるので、座標BからK番目に近い点の座標を求めなさい。
点の数とクエリの数は最大10^5個。高速な処理が求められます。

解答（不正解１）

N, Q = map(int, input().split())
A = list(map(int, input().split()))
for _ in range(Q):
    b, k = map(int, input().split())
    print(sorted([abs(i - b) for i in A])[k-1])

高速な処理が思いつかなかったのでいったん低速な処理でコードを書いて提出してみました。
数直線上の点をリストAに格納。
それぞれの点とクエリで与えられた座標Bとの距離を計算してソート。そしてK番目の要素を出力します。
結果はもちろんTLE（実行時間超過）、実行時間制限が2秒のところ3324 msかかっていました。

解答（不正解２）

import bisect
N, Q = map(int, input().split())
A = list(map(int, input().split()))
A.sort()
for _ in range(Q):
    b, k = map(int, input().split())
    border = bisect.bisect_left(A,b)
    print(sorted([abs(i - b) for i in A[max(border - k,0):border + k]])[k-1])

先ほどの回答からなんとかして実行時間を短くできないかと試したコードです。
二分探索（後で詳しく触れます）を行って座標Bを数直線上の点配列Aの中に置いたら何番目の位置になるのかを求め、そこから前後K個までの要素を抜き出します。
そして抜き出し要素の中から先ほどの回答と同様座標Bとの距離を求めてソートしてＫ番目の座標を出力しています。
しかしこのコードもTLE。実行時間は3326 msと変わりませんでした。前後K個までの要素を抜き出す処理を加えても結局クエリで与えられるKが大きいと意味がないのです。
そしてここでタイムアップとなりました。

解答

import bisect
N, Q = map(int, input().split())
A = list(map(int, input().split()))
A.sort()
for _ in range(Q):
    b, k = map(int, input().split())
    dist_low = -1
    dist_high = max(b - A[0], A[-1] - b) + 1
    while dist_low  + 1 < dist_high:
        dist_mid = (dist_low + dist_high) // 2
        c = bisect.bisect_right(A, b + dist_mid) - bisect.bisect_left(A, b - dist_mid)
        if c >= k:
            dist_high = dist_mid
        else:
            dist_low = dist_mid
    print(dist_high)

コンテスト終了後に解説を見ながら書いたコードです。というかほとんど丸パクリです。

座標Bからとある距離までの範囲にいくつ点が存在するか？は二分探索で求められます。
そして「座標Bからとある距離までの範囲に存在する点の数」がKになる距離はいくらか？で二分探索を行えば座標BからK番目に遠い点が求められます。
つまり二重に二分探索をしているということですね。

二分探索とは

二分探索でググればたくさん出てきますが一応軽く触れておきます。
二分探索はざっくり言うと、ソートされた配列に対してある値がその配列内のどこに入るのかを高速で計算するアルゴリズムです。

[0, 2, 3, 5, 6, 7, 8]の中にソートを崩さずに4を入れるならどこに入れるか考えます。
まずリストの中央の値、5を取ります。
5は4より大きいです。
よって4を入れたい場所は5よりも左側にあります。

次は6の左側[0, 2, 3]の中央の値、2を取ります。
2は4より小さいです。
よって4を入れたい場所は2より右側にあります。

次は2より右側[3]の中央の値、3を取ります。
3は4より小さいです。
よって4を入れたい場所は3の右側です。

といった具合に配列の目標の値が中央の値の左右どちら側にあるのかという比較を繰り返すアルゴリズムです。
半分、また半分と繰り返すので計算量はO(log2 N)と高速です。

D問題の解答に戻ります。
pythonには二分探索用のライブラリ、bisectが用意されています。単純な二分探索であればこれがそのまま使えます。
解答のコードでは二重に二分探索を行っています。
内側の二分探索「座標Bからある距離までの範囲にいくつ点が存在するか？」はbisectが使用できます。
外側の二分探索「「座標Bからとある距離までの範囲に存在する点の数」がKになる距離はいくらか？」については数値の比較に内側の二分探索を使用するので自前で実装する必要があります。

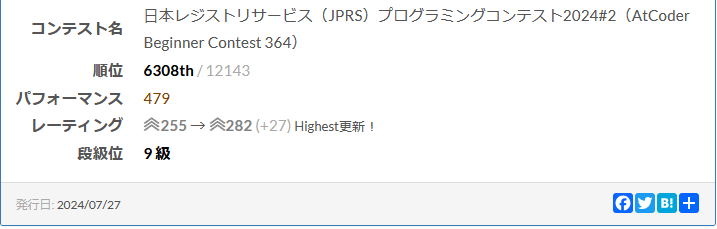
コンテスト結果

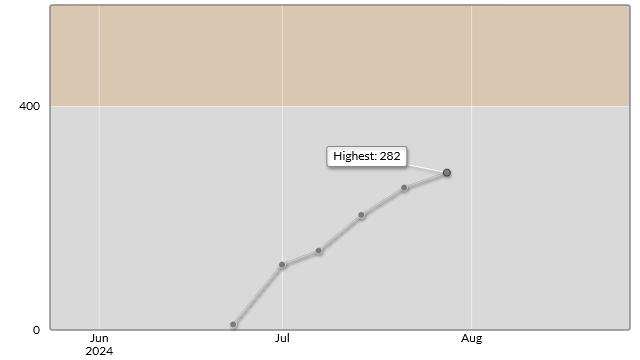
今回のD問題は解法も思いつかなかったのが悔しいところです。
最近読んだ本で二分探索が二重になっているパターンの例題があったのですが読むだけで解いていませんでした。やっぱり実際に問題を解いてみないと身に付きませんね。
D問題は壁だったようで順位表を見てみると私と同じC問題までの3完の人が多かったです。
同じ得点でも解答までが早かった人はパフォーマンス（推定レート）が1080でした。
となるとB問題で無駄に時間を使ったのが痛い…

おわりに

次回はABC365の記事を投稿します。
本ブログを通じて私と一緒に競技プログラミングの世界を楽しんでいただければ幸いです。
また、各種ご支援させていただきますので、お気軽に「お問い合わせフォーム」よりお問い合わせください。

お問い合わせ
　業務実績　

関連記事